Las líneas trigonométricas (dibujo circulo unitario)

Las

 líneas trigonométricas.

EJERCICIOS GEOMETRIA PLANA PAG 24-25

Lecciones Construyete

LECCIONES CONSTRUYETE

LECCION 1.6

LECCION 2.6

LECCION 3.6

LECCION 4.6

LECCION 5.6

LECCION 6.6

Resumenes de la Rubrica

RESÚMENES 

• Resumen : Clasificación y formas de medición de algunos .Conversión de ángulos
• Resumen: Razones trigonométricas.
• Resumen : Ángulos de elevación y de depresión.
• Mapa cognitivo de aspectos comunes entre los conceptos de los ángulos de elevación y los ángulos de depresión.
• Resumen: Las características para la medición de ángulos en trigonométrica (ángulos de referencia)
• Mapa cognitivo de secuencias para representar y calcular algunos de referencias.
• Resumen del circulo unitario y funciones trigonométricas
•  Matriz de clasificación de las características delas gráficas de funciones trigonométricas.
• Resumen de la ley de senos y la ley de los cosenos
• Mapa cognitivo tipo satélite de la ley de los senos y cosenos.

TRABAJO 1.

   CLASIFICACIÓN Y FORMAS 

DE ÁNGULOS

 

 ¿QUE ES UN ANGULO?

Un ángulo en el plano se define como la abertura formada por dos semirrectas que tienen en común su origen, éstas se llaman lados del ángulo y el punto en común se denomina vértice.

FORMAS DE MEDICIÓN

 Para la medición de ángulos existen dos sistemas importantes: el sexagesimal y el internacional.

• La unidad de medida para el sistema sexagesimal es el grado que es el resultado de dividir una circunferencia entre 360 partes iguales ,un grado son 60 minutos y un minuto son 60s.

• La unidad de medida del sistema internacional es el radian , que es la medida del angulo central cuando la  longitud del arco es igual al radio 

• La unidad de medida del Grado centesimal  es la unidad angular que divide la circunferencia en 400 grados centesimales.  

• La unidad de medida del Horario es su unidad de medida es el ángulo de 1 hora, que equivale a la sexta parte del ángulo recto.

Relación entre los Sistemas de medición de 

ángulos:

180º -------- π rad. ----------- 200G----------- 12 h

1 º es la forma de simbolizar un grado sexagésima

1º = 60 minutos = 60′ (un grado se divide en 60 partes iguales, cada una de ellas se llama minuto) 

1′ = 60 segundos = 60”  (un minuto se divide en 60 partes iguales, cada una de ellas se llama segundo)

  

Uso de la calculadora en trigonometría

Debemos tener en cuenta que la calculadora usa 3 modos distintos para trabajar con ángulos: DEG - GRA - RAD

DEG : modo grados sexagesimales (el más habitual)

RAD : modo radianes

GRA : modo gradianes (grados centesimales). Este tipo de medida no suele usarse (una circunferencia tiene 400 grados centesimales).

 Equivalencias:                                                    

•  Un ángulo de 180° equivale a π radianes

• Un ángulo de 360° equivale a 2π radianes

• Vale recordar que el número π ≈ 3,14159265359…                  

TRABAJO 2.

RAZONES TRIGONOMÉTRICAS

En un triángulo rectángulo podemos establecer las razones o cocientes entre sus lados. Para el triángulo rectángulo que se muestra a continuación tenemos sus elementos:

La hipotenusa, el lado opuesto al ángulo recto, es el lado más largo del triángulo rectángulo; los catetos son los lados que forman el ángulo recto, los ángulos se nombran  con letras mayúsculas y los lados se nombran con la misma letra, pero minúscula, de acuerdo al ángulo opuesto.

Las razones trigonométricas se definen con respecto a un ángulo agudo, en tal  caso los catetos se designan de la siguiente manera: el cateto que está al frente del ángulo se denomina cateto opuesto, el cateto que forma el ángulo, se denomina cateto adyacente, como se muestra.

Las tres primeras  razones trigonométricas para el ánguloA, llamado en este caso ángulo α son:

• Seno del ángulo A = sen A = cateto opuesto / hipotenusa = a / b

• Coseno del ángulo A = cos A = cateto adyacente / hipotenusa = c / b

• Tangente del ángulo A = tan A = Cateto opuesto / cateto adyacente = a / c

No obstante, no podemos pasar por alto que también existen las razones trigonométricas en una circunferencia. En este caso, hay que tener en cuenta diversos datos de interés e importancia como estos:

-La circunferencia goniométrica es la que tiene su centro en lo que es el origen de las coordenadas, mientras que su radio es la unidad.

-En dicha circunferencia los mencionados ejes de coordenadas lo que hacen es delimitar a cuatro cuadrantes, apareciendo triángulos semejantes.

-En cuanto a las razones trigonométricas que pueden tener lugar en general podemos determinar que existen distintos tipos de relaciones, tales como los ángulos suplementarios, los ángulos complementarios, los ángulos opuestos, los ángulos que difieren en 180º, los ángulos mayores de 360º, los ángulos negativos, los que suman 270º e incluso los que difieren en 90º, entre otras modalidades.

-Asimismo existen en este caso razones trigonométricas del ángulo mitad o las llamadas de ángulo doble.

Coseno del ángulo A = cos A = cateto adyacente / hipotenusa = c / b

Tangente del ángulo A = tan A = Cateto opuesto / cateto adyacente = a / c

TRABAJO 3.

ANGULOS DE ELEVACION Y DEPRESION.

  

Son ángulos formados por dos lineas imaginarias llamadas :lineas visual o linea de vision y la linea horizontal.
En estos casos,el observador se encuentra por debajo del objeto observado o bien,se encuentre por encima de dicho objeto.
La linea de vision es la linea que va desde el ojo de un observador hasta el objeto de interés.
La linea horizontal es una linea paralela a la superficie del agua.
El angulo de elevacion (o depresion) es un angulo formado por la linea horisontal y la linea de vision localizada arriba (o abajo) de la linea horizontal, pero en el mismo plano vertical.}
Asi en este ejemplo el observador divisa un aeroplano arriba de la horizontal y el angulo formado por la horizontal y la linea de vision se denota como angulo de elevacion. Al apuntar a un automovil,el angulo que forma la linea de vision con la horizontal e sun angulo de depresion.

TRABAJO 4.

 

TRABAJO 5

CARACTERÍSTICAS PARA LA MEDICIÓN DE ÁNGULOS EN TRIGONOMÉTRICA (ÁNGULOS DE REFERENCIA)

¿QUE ES?

Un ángulo de referencia es un ángulo agudo positivo que representa un ángulo θ de cualquier medida. Éste es el ángulo más pequeño formado entre el lado terminal de θ y el eje x. Siempre utilizamos éste último como su marco de referencia y el procedimiento para medirlo dependerá del cuadrante en el que se encuentre θ.

Ángulo de referencia

Digamos que θ  es un ángulo de ningún cuadrante en posición estándar. Su ángulo de referencia es el ángulo agudo a formado por el lado terminal de θ y el eje horizontal.

      Cuadrante I:  El ángulo dado y el ángulo de referencia son el mismo ángulo.

        α = θ

      

      Cuadrante II:  α = π – θ (radianes)

        α  = 180°– θ (grados)

      

      Cuadrante III: α  =  θ – π (radianes)

         α = θ – 180° (grados)

      

      Cuadrante IV:  α = 2 π – θ (radianes)

   α = 360° – θ   (grados)

      

TRABAJO 6.

TRABAJO 7.

CIRCULO UNITARIO Y FUNCIONES TRIGONOMÉTRICAS.

La circunferencia gonometrica,trigonometrica,unitaria o "circulo unidad" es una circunferencia de radio uno ,normalmente con su centro en el origen (0,0) de un sistema de coordenadas cartesianas, de un plano eudideo .Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas mediante la representación de triángulos rectángulos auxiliares.

Valores de las funciones trigonométricas para arcos comunes

Las funciones trigonométricas para arcos comunes se obtienen a partir de la circunferencia unitaria. Los arcos comunes expresados en grados son o,30,45,60 y 90  grados. En la siguiente figura veraz la tabla que resume el valor de las seis funciones trigonométricas para cada uno de estos arcos.

Valores Arcos Comunes

Funciones trigonométricas en el circulo.

 

Circulo Unitario

TRABAJO 8

MATRIZ DE CLASIFICACIÓN DE 

LAS CARACTERÍSTICAS DE LAS GRÁFICAS DE 

FUNCIONES TRIGONOMÉTRICAS

Algunas de las propiedades de una gráfica de las funciones trigonométricas son: dominio, máximo, asíntotas, periodo, alcance, etc.

Las funciones trigonométricas son: y=sen(x), y=cos(x), y=tan(x), y=cot(x), y=csc(x) o y=sec(x), en donde lo que está en el paréntesis es el dominio y “y” es el alcance.

CARACTERÍSTICAS DE LA GRÁFICA DE  y = sen(x)

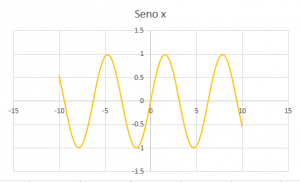
El ciclo de la función seno comienza en 0 y termina en 2π.

• Dominio: el conjunto de números reales
• Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
• Cruza el eje de “y” en (0,0)
• El eje de referencia es: eje “x”.
• El punto máximo es:  (π/2,1)
• El punto mínimo es: (3π/2,-1)

Su período: 2π.

CARACTERÍSTICAS DE LA GRÁFICA DE  y = cos(x)

• El ciclo fundamental de la función coseno del ángulo comienza en 0 y termina en 2π.
• Dominio: el conjunto de números reales.
• Alcance: el conjunto de números mayores o iguales que -1 hasta los números menores o iguales que 1.
• Cruza el eje de “y” en: (0,1)
• El eje de referencia es: el eje “x”
• El punto máximo es:  (0,1) y (2π,1)
• El punto mínimo es: (π,-1)
• Su período: 2π

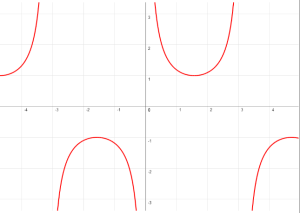
CARACTERÍSTICAS DE LA GRÁFICA DE  y = tan(x)

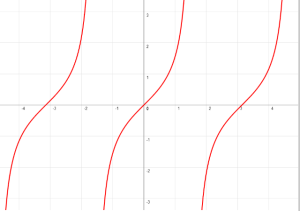
• El ciclo fundamental de la función tangente del ángulo comienza en -π/2 y termina en π/2.
•  Tiene asíntotas en el ciclo.
• Dominio: toda x diferente a (π/2)±nπ
• Alcance: el conjunto de todos los números reales.
• Cruza el eje de “y” en  (0,0)
• El eje de referencia es: el eje “x”
• El punto máximo es:
• El punto mínimo es:
• Su período: π
• Asíntotas: x=±π/2
•  

CARACTERÍSTICAS DE LA GRÁFICA DE  y = cot(x)

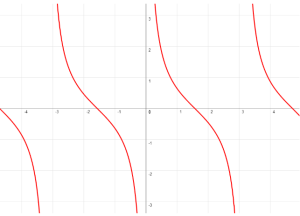
• El ciclo fundamental de la función cotangente del ángulo comienza en 0 y termina en π.
• Tiene asíntotas en el ciclo.
• Dominio: toda x diferente a ±nπ
• Alcance: el conjunto de todos los números reales.
• No cruza el eje de “y”
• El eje de referencia es: el eje “x”.
• Su período: π
• asíntotas: x=±nπ

CARACTERÍSTICAS DE LA GRÁFICA DE  y = sec(x)

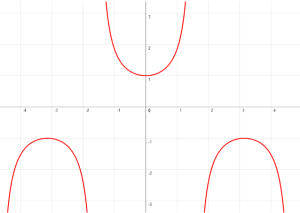
• El ciclo fundamental de la función secante del ángulo comienza en -π/2 y termina en 3π/2.
• Tiene tres asíntotas verticales.
• Dominio: el conjunto de números reales excepto los múltiplos impares de π/2
• Alcance: el conjunto de todos los números reales menores menores o iguales que –1 y todos los números mayores o iguales que 1
• Cruza el eje de “y” en (0,1)
• El eje de referencia es: el eje “x”
• El punto máximo es:  (π,-1)
• El punto mínimo es:  (0, 1)
• Su período: 2π
• Asíntotas: x=-π/2, x=π/2 y x=3π/2

CARACTERÍSTICAS DE LA GRÁFICA DE  y = csc(x)

• El ciclo fundamental de la función cosecante del ángulo comienza en 0 y termina en 2π.
• Tiene tres asíntotas.
• Dominio: el conjunto de números reales excepto los multiplos impares de π/2
• Alcance: el conjunto de todos los números menores o iguales que -1 y todos los números mayores o iguales que1
• Cruza el eje de “y” en (0,1)
• El eje de referencia es: el eje “x”
• El punto máximo es:   (π,-1)
• El punto mínimo es: (0, 1)
• Su período: 2π
• Asíntotas: x=-π/2, x=π/2 y x=3π/2

TRABAJO 9

LEY DE SENOS Y DE COSENOS.

LEY DE SENOS:

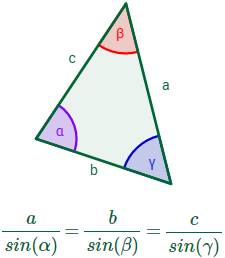La ley de los senos es la relación entre los lados y ángulos de  triángulos no rectángulos (oblicuos). Simplemente, establece que la relación de la longitud de un lado de un triángulo al seno del ángulo opuesto a ese lado es igual para todos los lados y ángulos en un triángulo dado. En resumen seria:
Los lados de un triangulo son proporcionales a los senos de los ángulos opuestos.

LEY DE LOS COSENOS

En triangulo el cuadrado de cada lado es igual a la suma de los cuadrados de los otros dos menos el doble producto  del producto de ambos por el coseno del angulo que forman.

TRABAJO 10.